擴展型卡爾曼濾波器(EKF)利用雅可比矩陣線轉換成線性函數,無跡卡爾曼濾波器(UKF)則以無跡轉換選擇西格瑪點。使用非線性轉換的UKF精確度高於EKF,適用極度非線性模型。
工作流程
(承上文)產生最佳的西格瑪點是執行UT之前,必須先完成的前置工作。跟EKF一樣,UKF也是從預估階段(Prediction Step)或時間更新(Time Update)開始的。在標準的UKF工作流程中,西格瑪點除了會通過非線性狀態預估函數𝑓,也會經過觀測模型(Observation Model)H。
此外,UKF也可能會使用控制向量(Control Vector)u。式子(10)至(12)是進行預估轉換(Prediction Transformation),使用經過非線性函數𝒳轉換後的新西格瑪點𝒳代入式子(11)和(12)中,求出x的預估均值和預估共變異數,後者還包含系統雜訊的共變異數(Covariance of the Process Noise)矩陣Q。式子(13)至(16)是進行觀測轉換(Observation Transformation),同樣是將經過非線性函數f轉換後的新西格瑪點𝒳代入觀測函數h,求出轉移矩陣ψ,然後計算y的預估均值和預估共變異數,後者還包含觀測雜訊的共變異數矩陣R。式子(16)是計算x和y之間的交互共變異數矩陣(Cross-Covariance Matrix)。
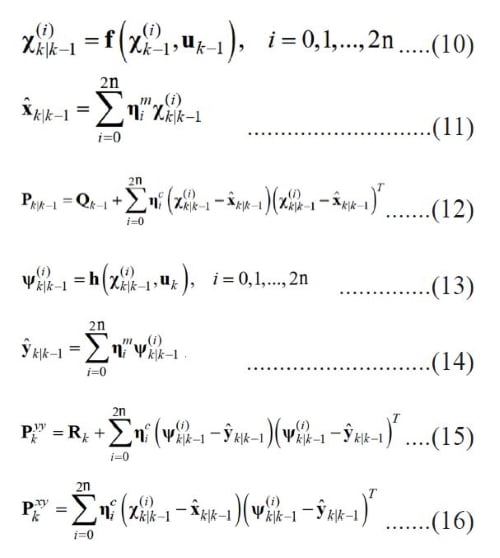
UKF在更新階段(Update Step)或測量更新(Measurement Update)時,先求出卡爾曼增益(Kalman Gain)K,如式子(17),然後使用K去更新預估狀態向量x_hat,如式子(18)。其中測量向量(Measurement Vector)yk是使用其它更精確的方法測得的。在下一個曆元k+1的預估階段,要產生新的西格瑪點時,就會用到這個x_hat。最後,使用K去更新預估狀態向量的共變異數矩陣Pk,如式子(19)。在下一個曆元k+1的預估階段,要產生新的西格瑪點時,也會用到這個Pk。反覆上述的流程,亦即反覆更新西格瑪點,目標就是將狀態向量的估測值極近似於系統的真實狀態。
通常,以處理雜訊的方法之不同,UKF可被區分為兩類:添加雜訊(Additive Noise)和不添加雜訊(Non-Additive Noise)。如圖3所示,將處理雜訊(Process Noise)或稱之為系統雜訊w代入狀態轉換函數𝑓內,成為𝑓的一個引數(Argument),這就是不添加雜訊的UKF。反之,則是添加雜訊的UKF。但不添加雜訊的UKF不是不處理系統雜訊w,而是在狀態轉換時,w就被𝑓處理了,而且在後續的方程式中,也看不到系統雜訊的共變異數矩陣Q。在添加雜訊的UKF中,系統雜訊w不被𝑓處理,但在求解預估狀態向量的共變異數矩陣Pk/k-1時,會加上Q這一項。
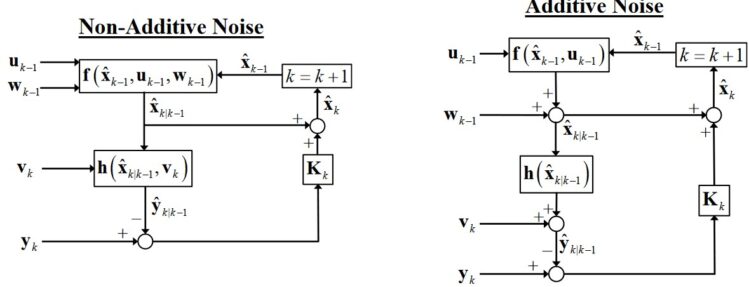
圖3 添加雜訊和不添加雜訊的UKF
操作範例
系統雜訊的共變異數矩陣Q的初始值設定與前篇的EKF程式一樣,但是依照式子(12)算出Pk|k-1的預估值。在完成一個曆元e運算迴圈之前,將求得的低軌衛星和地心之間的距離和實測的精確距離相減後,再取平方,亦即(S_collect(e)-r_precise(e)*10^3)^2,這就是新的Q矩陣對角線上的距離雜訊之變異數;另將曆元e時求得的低軌衛星和地心之間的距離與在曆元e-1時求得的低軌衛星和地心之間的距離相減,然後除以時間間隔dt,再取平方,亦即((S_collect(end)-S_collect(end-1))^2)/dt^2,此值就是新的Q矩陣對角線上的速度雜訊之變異數。
利用Matlab軟體的chol函式求出共變異數矩陣P的平方根sP,再依照式子(5)算出新的西格瑪點chi_p。然後,chi_p與狀態轉換矩陣phi相乘得出預估的西格瑪點chi_m,再依照式子(11)和(12)算出預估狀態向量的均值x_m和代表誤差的共變異數矩陣P_m。