擴展型卡爾曼濾波器(EKF)利用雅可比矩陣線轉換成線性函數,無跡卡爾曼濾波器(UKF)則以無跡轉換選擇西格瑪點。使用非線性轉換的UKF精確度高於EKF,適用極度非線性模型。
擴展型卡爾曼濾波器(Extended Kalman Filter, EKF)主要是使用雅可比矩陣(Jacobian Matrix),將非線性函數轉換成線性函數,然後傳播共變異數矩陣(Covariance Matrix)和狀態向量(State Vector)。無跡的卡爾曼濾波器(Unscented Kalman Filtering, UKF)則是使用非線性的無跡轉換(Unscented Transformation, UT),選出數量最少但效能最佳的西格瑪點(Sigma Point),透過它隨機傳播共變異數矩陣和狀態向量。由於UKF是使用非線性轉換,所以,一般而言,UKF的精確度高於EKF。當狀態轉換模型和觀測模型極度非線性化時,使用EKF預估低軌通訊衛星的座標的誤差量將增大,此時必須改用UKF或其它方法。
西格瑪點的選定
UKF和EKF兩者最大的不同是:EKF使用偏微分求解共變異數(Covariance),是屬於分析法,而UKF是使用統計法。圖1是EKF與UT的樣本均值(Mean)和共變異數傳播方式之比較。UKF的工作流程大致可區分為三個階段,如圖2所示。首先是無跡轉換,或稱作西格瑪點轉換。在狀態轉換前,須先選出西格瑪點,經非線性轉換後,再求出這些西格瑪點所代表的狀態向量的均值和共變異數。
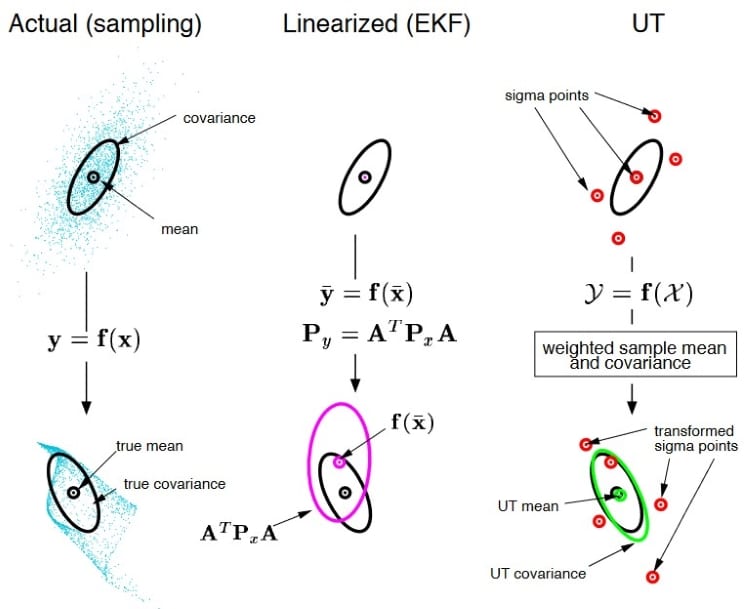
圖1 EKF與UT的樣本均值和共變異數傳播方式之比較
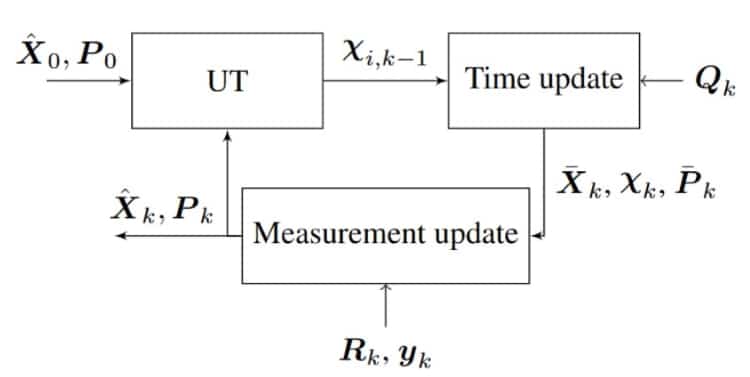
圖2 UKF的工作流程
假設有一個非線性狀態預估轉換方程式y=(x),x和y都是n*1大小的向量,輸入的隨機變數x是常態分布的,x也稱為狀態向量(State Vector)。μ或x_hat是x的預估均值(Estimated Mean),或稱之為x的期望值(Expected Value)E(x)。Px或Σ是x的共變異數矩陣。對一個有n個變數的機率分布函數(Probability Distribution Function, PDF)𝒩(μ,Σ)而言,需要至少2n+1個西格瑪點,其中一個是均值,其餘對稱地分布於均值附近。從PDF中選出西格瑪點時,需要利用科列斯基分解(Cholesky Decomposition),將一個共變異數矩陣P或正定矩陣(Positive Definite Matrix)Σ分解成下三角矩陣(Lower Triangular Matrix)L和L的共軛轉置(Conjugate Transpose)LT或L*之乘積,L的對角線上的元素都是正實數,如式子(1)所示。

基本上,科列斯基分解是一種開根號運算,亦即sqrt(Σ)=L。所以分解Σ實際上就是計算變異數(Variance)σ²的平方根,即求出標準差(Standard Deviation, SD)σ。第一個西格瑪點x0是設為PDF的均值,其餘的西格瑪點是某係數(Factor)乘以經科列斯基分解得出的L矩陣之積與PDF的均值相加或相減,如式子(2)所示。
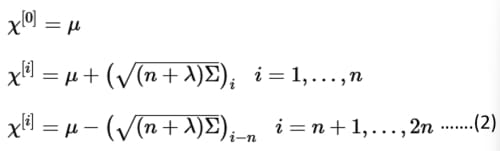
西格瑪點的擴散(Spread)規模,或者說先驗的(a Priori)隨機變數分布的可靠度(Confidence Level),主要是由α、β、κ三個純量參數(Scaling Parameter)決定的。這些參數能決定西格瑪點的擴散程度,其中α最具影響力,α的值介於10^-4到1之間。較小的α會造成西格瑪點的分布很緊密;反之,西格瑪點的分布會較為分散。β提供先驗的隨機變數的分布資訊,在常態分布的情況下,β=2是最佳的。κ通常設為0。此外,使用α、β、κ可以定義另一個純量參數λ,以及表示均值係數的權重向量(Weight Vector)ηm和表示共變異數係數的權重向量ηc。λ是由式子(3)計算得出,決定λ的參數包含α、n、k。而ηm和ηc是由式子(4)計算得出。式子(2)中的𝒳代表西格瑪點,它有2n+1個元素,亦即有2n+1個列,式子(5)是將式子(2)中的𝒳以向量形式表示。
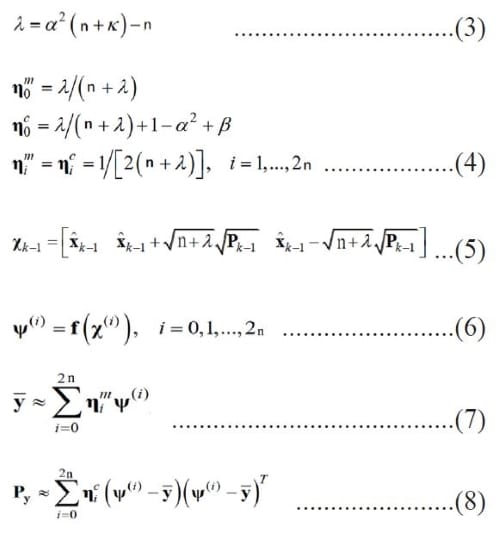
下面舉出一個求出西格瑪點的實例。表1是先前使用最小平方法(Least-Squares Method)建立的動力學模型(Kinetics Model)求出低軌通訊衛星的座標值和速度的預估數據,座標單位是公尺。表2是使用其它更精確的方法,測得的低軌通訊衛星的座標值,灰字部份是利用曆元k和曆元k+1之間的座標差除以10秒求得的速度。10秒就是曆元k和曆元k+1之間的時間差,計算公式是:(xp(2)-xp(1))/dt, (yp(2)-yp(1))/dt, (zp(2)-zp(1))/dt,其中xp、yp、zp代表座標值,xp(1)代表在曆元k時測得的X軸座標值,xp(2)代表在曆元k+1時測得的X軸座標值,dt等於10秒。表2的座標單位和表1的不同,它是以1000公里為單位。表1所列的數據是狀態向量x。表2所列的數據是狀態向量x的期望值μ,代入下列公式,即可以求出x的變異數Var(x)。
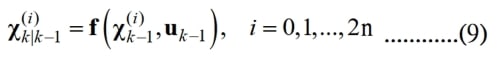

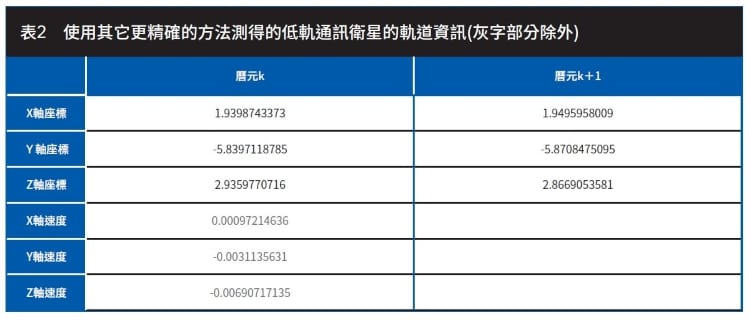
若只取表2的數據至小數點第五位,代入上式,可得出Var(x)的值為:[0.0000003249e12 0.000004e12 0.00000784e12 0.0000000009e12 0.0000000001e12 0.000000000049e12]。因Var(x)是共變異數矩陣P0的對角值,因此可得出P0為:diag[0.0000003249e12 0.000004e12 0.00000784e12 0.0000000009e12 0.0000000001e12 0.000000000049e12],此處都換成以公尺為單位。因為P0=LLT,如式子(1),所以,L=sqrt(diag[324900 4000000 7840000 900 100 49])。開根號之後,可以得出L=diag[570 2000 2800 30 10 7]。然後,將α=1、β=2和κ=0代入式子(3)得出λ=0。將λ代入式子(2),可得出西格瑪點𝒳。此外,利用式子(4)可得出ηm=[0 0.08333 0.08333 0.08333 0.08333 0.08333]和ηc=[0 0.08333 0.08333 0.08333 0.08333 0.08333]。
KF系列技術是源自遞迴的貝葉斯預估(Recursive Bayesian Estimation)或稱之為貝葉斯濾波器(Bayes Filter),它是以通用的機率方法(Probabilistic Approach)反覆計算,來預估未知的PDF。若隨機變數是正常分布,且狀態轉換是線性的情況下,貝葉斯濾波器等於KF。若隨機變數是正常分布,狀態轉換是非線性的,則貝葉斯濾波器等於EKF或UKF。因此在卡爾曼濾波器初始化時,可用不精確的猜測方法來設定代表預估誤差的初始共變異數矩陣P0。
當卡爾曼濾波器執行至下一個測量更新時,預估的狀態向量和共變異數矩陣會被更新,此時,變異數可能改變了,新的共變異數矩陣Pk不一定是由Var(x)=(x-μ)^2產生,有可能是由Var(x)=E[(x-μ)^2]產生的。所以,Var(x)=(x-μ)^2是一種特殊的猜測方法,不是求變異數的通用公式,Var(x)=E[(x-μ)^2]才是求變異數的通用公式。運算子E是代表求期待值或均值的意思。